Inclusion Exclusion Principle Problems With Solutions Pdf

50 A B C - A B - A C - B C 25 Or 25 A B C - A B - A C - B C. Then PA1 A2 An Xn i1 PAi X i.

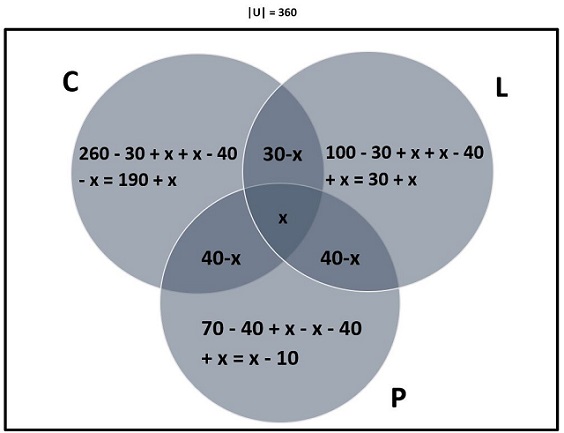
Inclusion Exclusion Principle Examples With Solutions

The Inclusion-Exclusion principle The inclusion-exclusion principle is the generalization of eqs.

. We can sell 75 apples. No calculation is necessary. Soon after it was selected as an IMO problem and before the competition was held some jury members found another way of solving the problem by applying the Principle of Inclusion and Exclusion PIE.

Principle of Inclusion and Exclusion is an approach which derives the method of finding the number of elements in the union of two finite sets. This can be done purely with the given information. 70 of students passed the Mathematics examination and.

Principle of Inclusion and Exclusion Problem Solving. This is equivalent to counting solutions to the equation x0 1 x 2 x 3 30 where x0 1 x 1 20 and thus x01x 2x 3 0. Consider two finite sets A and B.

The principle of inclusion and exclusion PIE is a counting technique that computes the number of elements that satisfy at least one of several properties while guaranteeing that elements satisfying more than one property are not counted twice. Finite sets and Venn diagrams are the standard methods of teaching this principle. The argument in part a implies that S.

With this inclusion-exclusion principle question the three sets can be defined as follows. In this regard by inclusion - exclusion principle 60 10 30 10 at least one color will be missing 3 - 3 90 10 possible outcomes thus the desired probability is Since there are 60 10 30 10 3 - 3 P at least one color is missing 90 10 0. After a grueling nationwide examination it was announced that.

1 Solutions to Inclusion-exclusion problems Let A 1A nbe events in a probability space. Find the value of N. To form such a study group we just need to choose at least 2 of the remaining 17 students.

1 and 2 to n sets. Inclusion-exclusion our equation is NP0 1 P 0 2 N NP 1 NP 2 NP 1P 2 100 20 1510 75. Then by the Inclusion-Exclusion Principle the number to be determined in the problem is given by A 1 A2 A3 S A1A2A3 A1 A2A1 A3 A2 A3 A1 A2 A3.

The Principle of Inclusion-Exclusion abbreviated PIE provides an organized methodformula to find the number of elements in the union of a given group of sets the size of each set and the size of all possible intersections among the sets. The answer is denoted by Nc 1 c 2 c 3 which is evaluated below. Instead of counting study groups that include at least one of Alicia Bob and Sue we will count study groups that dont include any of Alicia Bob or Sue.

Solve practice problems for Inclusion-Exclusion to test your programming skills. P r are all prime numbers. In order to do so for any 1 i1 ik n we have to compute Ai1 Ai2 Ai k.

The virtue of this approach is that Ai1 Ai2 Ai k is indeed computable. If there are 50 first-year students that are taking both Calculus and Algebra how many first-year. Be the set of students who have taken a course in.

Let S 1 2 100 and N S 100. Let Nbe an integer such that N pa 1 1 p a2 2 p a 3 3 p r r where p 1p 2p 3. I cant see how to choose the sets that would lead to a nice and simple solution based on it but I too would be interested to see it.

In fact Ai1 Ai2 Ai k. S 1 is the number of solutions in which x 1 20. The first step is to formally identify the sets and indicate the number of elements in each.

The inclusion and exclusion connection and disconnection principle is mainly known from combinatorics in solving the combinatorial problem of calculating all permutations of a finite set or other combinatorial problems. Let U denote the entire set of patients. The inclusion exclusion principle implies that i 3 i1 S i X3 i1 S S 1 2S 3S S.

Let P 1P 2P 3 be the property of the solution when P 1 x 1 6 P 2 x 2 6 1. A cup B cup C A B C - A B - A C - B C A B C Substituting for the knows values. Y 1 Y 3 Y 4 ifandonlyify 1 12y 3 17andy 4 31.

The inclusion and exclusion connection and disconnection principle is mainly known from combinatorics in solving the combinatorial problem. Let A1 A2An be a sequence of nevents. By the principle of inclusion-exclusion jABSj 3 219 1 3 218 217.

Also go through detailed tutorials to improve your understanding to the topic. Let j denote P 1 i 1 Inclusion-Exclusion formula where none of the events happen. What is the minimum percentage of.

Principle of Inclusion and Exclusion An Illustrative Example Determine the number of integers n 1 n 100 which are not divisible by 2 3 5. By the inclusion-exclusion principle the number of onto functions from a set with six elements to a set with three elements is. The inclusion exclusion principle is designed to compute A1 An.

Ensure that you are logged in and have the required permissions to access the test. It doesnt really need the Inclusion-Exclusion Principle here one only set is included in the other. University of Windsor Mathematics Contest Practice Problems Principle of Inclusion-Exclusion and Pigeonhole Principle Solutions 1.

Now for the other solution. Let us analyze the summands on the right side in turn. 0395 With replacement at least one color will be missing 3 60 10 - 3 30 10 and there are 90 10 possible outcomes.

Suppose there are 200 first-year students 100 of which are taking Calculus and 70 of which are taking Algebra. Define three conditions as follows. 60 of students passes the Science examination.

The principle of Inclusion-Exclusion states that. Aftercomputingthesizesofthevariousintersectionsusingbarsandstarsthe answeris 674 4. This is used for solving combinations and probability problems when it is necessary to find a counting method which makes sure that an object is not counted twice.

The solution of the above problem given by the proposer involves some complicated recurrence relations which make the problem looks hard. Note that S 3 10 3101 10 12 10 66 A1 3 6 361 6 8 6 28 A2 3 5 351 5 7 5 21 A3 3 4 341 4 6 4 15 A1 A2 3 1 311 1 3 1 3 A1 A3 3 0. A new employee checks the hats of.

Let S i set of integers less than N which are divisible by p i 1 i r So jS i j Np i Hence by applying principle of inclusion and exclusion. 564 3 How many solutions does the equation x 1 x 2 x 3 13 have where x 1x 2 and x 3 are nonnega-tive integers less than 6. An underlying idea behind PIE is that summing the number of elements that satisfy at least one of two categories and subtracting.

Inclusion Exclusion Principle Examples With Solutions

The Principle Of Inclusion Exclusion Basic Example Youtube

Inclusion Exclusion Principle Examples With Solutions